자연대 홍보기자단 자:몽 6기 | 유경민

 
예나 지금이나, 사람들에게 미래를 예측하는 일은 아주 중요하다. 원시인들은 내일 날씨가 어떨지, 이번 주에는 사냥감을 잡을 수 있을지 알고 싶어 했으며, 현대인들은 내일 주가가 오를지, 휴가 때에 날씨가 좋을지 알고 싶어 한다. 각자가 처한 사정이 어떻든 간에, 다가오는 미래를 정확히 알 수 있다는 것은 큰 이점임에 틀림없다. 그렇지만 자연은 주식 투자자들의 일확천금이나 직장인들이 즐거운 휴가를 보내는 것이 마음에 들지 않았는지, 미래를 정확히 예측할 수 없도록 장치를 만들어 두었다. 그 장치는 바로 ‘다체 문제 (Many body problem)’라는 난관이다.
 
다체 문제가 등장한 시점은 뉴턴이 만유인력 법칙을 정립한 이후, 행성의 운동을 물리적으로 기술할 수 있게 되었을 때이다. 만약 태양계가 태양과 지구로만 구성되어 있었다면 다체 문제가 등장하기까지는 시간이 더 걸렸을 것이다. 하지만 태양계에는 태양과 지구 외에도 달, 금성, 목성 등 위성 및 다른 행성들이 있고, 화성과 목성 사이에 주로 분포하는 소행성들 또한 그 각각이 지구에 중력을 작용하고 있다. 태양의 질량이 다른 천체들에 비하여 압도적으로 크기 때문에 태양과 지구만의 계를 상정하여도 지구의 운동을 유의미한 수준에서 설명하는 데에는 문제가 없었다. 그렇지만 물리학자들은 여기서 멈추지 않고, 비록 그 크기가 태양의 중력에 비해 매우 작기는 하지만, 태양 외에 다른 천체들이 작용하는 중력까지 포함하여 지구의 운동을 서술하고자 하였다.
 
그러나, 세 개 이상의 천체 사이에 존재하는 상호작용을 모두 고려한 역학 시스템은 태양과 지구 사이의 중력만을 고려한 시스템에 비해 너무나도 어려웠다. 태양과 지구만의 계를 생각하면, 태양과 지구는 두 천체의 질량중심을 기준으로 타원 궤도 운동을 한다. 그러나, 다른 천체가 태양과 지구에 중력을 작용하게 되면 태양과 지구의 궤도 형태를 쉽사리 예측하기가 어렵다. 게다가, 태양과 지구 또한 해당 천체에 중력을 작용하기 때문에, 그 천체의 위치도 종잡을 수 없이 바뀔 것이다. 이처럼 천체가 세 개만 되어도 고려해야 하는 상호작용이 1개에서 3개로 늘어나는데, 그보다 더 많은 천체로 이루어진 계는 말할 것도 없다. 이처럼 세 개 이상의 서로 상호작용하는 물체의 운동을 정확히 기술하려는 것을 다체 문제라고 하며, 많은 연구자들이 그 해결을 위하여 노력하였다. 결국 다체 문제의 일반적인 해를 구할 수 없다는 것을 프랑스의 수학자 앙리 푸앵카레가 1890년에 증명하였고, 현재는 다체 문제를 풀기 위한 일반적인 방법을 찾는 것이 아니라 몇몇 특수한 혹은 근사가 가능한 상황에서의 해를 찾으려는 연구만이 진행되고 있다.
 
다체 문제의 일반적 해결 불가능성이 시사하는 바는, 여러 개의 상호작용하는 물체로 이루어진 계가 시간이 지남에 따라 어떤 운동을 할지 일반적으로 예측할 수 없다는 것이다. 따라서 다체 시스템에서 ‘미래를 예측’하기 위해서는, 해당 시스템의 초기 조건이 운 좋게도 특수한 해를 구할 수 있는 경우이기를 기대하거나, 아니면 적절한 근사를 통하여 참값과는 약간 차이가 있지만 그래도 합리적인 해를 구하는, 둘 중 한 가지 길을 택해야 한다. 전자의 경우에는 정확한 해를 구할 수 있겠지만 계의 초기 조건이 특수해를 내놓을 확률이 매우 희박하다는 한계가 있고, 후자는 해의 정확도를 일정 부분 포기해야 하지만 일반적인 시스템에 대해서 얼마든지 적용할 수 있다는 점에서는 실용적이다.
 
푸앵카레의 증명 이후 다체 문제는 그저 해결 불가능한 문제쯤으로 간주되다가, 러더퍼드가 1911년 알파 입자 산란 실험을 통하여 원자핵의 존재를 밝힌 뒤 다시 중요한 개념으로 부상하기 시작했다. 서로 중력을 작용하며 운동하는 행성과 마찬가지로, 서로 전기력을 작용하는 원자 내의 핵과 전자의 움직임 또한 다체 문제에 해당하기 때문이다. 그러나 러더퍼드가 제시한 원자 모형에 모순이 있음이 확인되고 양자역학이 발전함에 따라, 미시 세계에서의 다체 문제는 거시 세계의 그것과 조금 다르다는 것이 밝혀졌다. 미시 세계와 거시 세계의 가장 큰 차이는 입자 또는 물체의 존재 방식을 기술하는 방식이다. 거시 세계에서는 물체가 존재하는 위치를 정확히 알 수 있지만, 미시 세계에서는 불확정성 원리가 유의미해지므로 입자의 존재 위치를 규정할 수 없고, 단지 파동함수라는 개념을 통하여 입자의 특정 지점에서의 존재 확률만을 알 수 있다. 이러한 근본적인 차이 때문에 미시 세계에서의 다체 문제에 대한 접근법은 거시 세계에서의 다체 문제와는 다를 수밖에 없었다.
 
미시 세계의 다체 문제를 다루는 것이 중요한 이유는, 대부분의 분자나 재료는 모두 여러 개의 핵과 전자로 이루어져 있기 때문이다. 따라서 특정 분자의 구조나 재료의 물성을 이론적으로 예측하기 위해서는 미시 세계의 다체 문제를 필수적으로 다루어야 한다. 월터 콘 (Walter Kohn, 1923-2016) 과 존 포플 (John Pople, 1925–2004) 은 미시 세계의 다체 문제에 관하여 연구하고 그를 바탕으로 컴퓨터를 통해 재료의 원하는 물성을 예측할 수 있는 방법론을 개발한 공로로 1998년 노벨 화학상을 수상하였다. 월터 콘이 루 샴 (Lu Sham, 1938-), 피에르 호헨버그 (Pierre Hohenberg, 1934–2017) 등과 함께 정립한 밀도범함수이론 (Density Functional Theory, DFT) 은 분자나 결정의 물리적ㆍ화학적 성질 등을 밝히는 이론적 토대가 되어 주었으며, 존 포플이 개발한 컴퓨터 기반의 양자화학 계산법은 밀도범함수이론을 통한 복잡한 계산을 실제로 구현할 수 있도록 하였다.
 
두 노벨상 수상자 중 월터 콘이 발전시킨 밀도범함수이론에 대하여 더 살펴보자. 여러 개의 핵과 전자로 이루어진 계를 해석하는 것은 다체 문제이므로, 푸앵카레의 증명에 의하여 해당 계의 물리량을 완벽히 구할 수는 없다. 이러한 계의 복잡성을 대변하는 것이 바로 다체 파동함수 (Many body wave function) 이다. 전자와 전자는 서로 상호작용하므로, 핵 주위에서 전자의 파동함수를 구하기 위해서는 각 전자의 위치와 스핀을 모두 파동함수의 변수로 설정해야 한다. 즉, 계가 총 N개의 전자로 구성되어 있다면, 각 전자의 위치와 스핀, 다시 말해 2N개의 변수를 모두 파동함수에 포함하여 계산해야 한다는 뜻이다. 이러한 다체 파동함수의 형태는 알려져 있지 않으며, 설령 그 형태가 주어져 있다 해도 계산이 너무 복잡하므로 다체 파동함수를 그대로 이용하여 원하는 물리량을 구하는 것은 사실상 불가능하다.
 
밀도범함수이론의 첫 번째 아이디어는, 다체 파동함수를 대신할 좀 더 간단하고 다루기 쉬운 물리량을 찾는 것이다. 그 이름에서도 알 수 있듯이, 밀도범함수이론에서는 특정 위치에서 전자를 발견할 확률‘밀도’를 다체 파동함수를 대신할 물리량으로써 이용한다. 호헨버그–콘 정리 (Hohenberg–Kohn theorem) [1] 는 계의 형태가 정해지면 그에 대응하는 다체 파동함수와 전자 밀도가 유일하게 결정되며, 다체 파동함수와 전자 밀도는 일대일대응한다는 것을 보인 정리이다. 이 정리는 전자 밀도를 다체 파동함수 대신 이용할 수 있도록 하는 수학적 기반이 된다.
 
그러나 전자 밀도는 본질적으로 다체 파동함수를 제곱한 물리량이기 때문에, 다체 파동함수에 비해 직관적이기는 하지만 여전히 그 형태를 명확히 알 수 없다. 이 문제를 해결하기 위하여, 전자 사이의 상호작용이 전혀 없는 유효 시스템 (Auxiliary system) 을 잡는다는 아이디어가 중요한 역할을 했다. 전자 사이의 상호작용이 하나도 없으면, 각 전자의 파동함수를 수소 원자의 오비탈처럼 취급할 수 있기 때문에 이러한 계에서는 밀도를 구하는 것이 훨씬 쉽다. 이때 전자 사이의 상호작용이 하나도 없음에도 불구하고, 전자 밀도가 전자 사이의 상호작용이 있는 원래 계와 완전히 동일한 가상의 계가 있다면, 이 가상의 계에서의 전자 밀도를 계산함으로써 결국 원래 계에서의 전자 밀도를 알 수 있다. 이러한 가상의 계를 유효 시스템이라고 하며, 원래 계와 밀도가 완전히 동일한 유효 시스템을 잡을 수 있음이 증명되어 있다. [2]
 
유효 시스템이라는 아이디어를 바탕으로, 밀도범함수이론의 기본이 되는 미분방정식인 콘–샴 방정식 (Kohn–Sham equations) 을 유도할 수 있다. [3] 콘–샴 방정식의 핵심은, 유효 시스템을 잡음으로써 각 전자를 서로 상호작용하지 않는 독립적인 입자로 취급할 수 있으며, 이 전자들이 수소 원자의 오비탈과 유사한 ‘콘–샴 오비탈 (Kohn–Sham orbital)’ 에 차곡차곡 들어간다고 간주할 수 있다는 것이다. 즉, 유효 시스템이 없었다면 매우 복잡하고 그 형태가 명확히 알려져 있지 않은 다체 파동함수를 이용한 슈뢰딩거 방정식을 풀어야 했지만, 유효 시스템을 도입함으로써 N개의 전자에 대한 비교적 쉬운 슈뢰딩거 방정식 N개를 풀어도 충분하다는 것이다. 콘–샴 방정식을 통하여 바닥 상태 계의 전자 밀도를 구할 수 있으며, 전자 밀도는 계의 총 에너지, 밴드 갭 (Band gap), 격자 상수 (Lattice constant) 등을 구하는 기반이 된다.
 
그러나 콘–샴 방정식은 교환–상관 (Exchange–correlation) 항이라는, 그 꼴이 명확히 알려지지 않은 항을 포함한다. 이 항은 밀도범함수이론을 통하여 특정 물리량을 계산할 때 그 정확도와 직결되는 매우 중요한 항이며, 이를 근사하기 위한 여러 방법론들이 연구되어 왔다. 그 대표적인 예시로는 LDA (Local–Density Approximation), GGA (Generalized Gradient Approximation) [4, 5], Meta-GGA [6, 7] 등이 있으며, 현재도 다양한 근사 방법론들이 연구, 제시되고 있다.
 
 

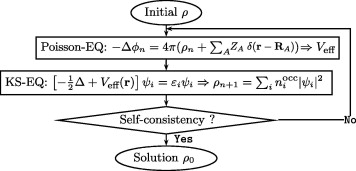
그림 1. 밀도범함수이론을 이용한 실제 계산 과정. (사진 = [8])

 
 
지금까지 살펴본 밀도범함수이론은 ‘자연을 바라보는 안경’이 될 수 있을 것이다. 안경을 쓰면 주변이 조금 왜곡되어 보이지만, 여러 사물을 더 선명하게 볼 수 있기 때문에 오히려 주위를 보는 데에 더 도움이 된다. 밀도범함수이론도 마찬가지다. 곧, 여러 근사와 수치해석 기법 때문에 구하고자 하는 물리량의 값이 실제와 약간 다를지라도, 그 값은 물리적으로 충분히 유의미한 것이기 때문에 분자 구조를 예측하거나 재료의 성질을 비실험적으로 파악하는 데에 도움이 된다는 것이다. 밀도범함수이론이 등장하기 이전까지, 재료의 특정 물성을 예측하기 위해서는 실험적 방법을 이용할 수밖에 없었다. 그러나 결함이 없고 순수한 재료를 합성하기 위해서는 많은 시간과 노력이 들며, 측정 과정에서 필연적으로 수반되는 오차가 있다는 단점이 있다. 밀도범함수이론은 이와 같은 실험적 방법의 단점을 잘 메꾸었고, 현재는 실험적 방법과 상호보완적으로 재료과학, 고체물리학 등의 분야에 다양하게 이용되고 있다.
 
어쩌면 누군가는 밀도범함수이론이라는 안경을 쓰지 않고도 자연을 선명하게 볼 수는 없는지 반문할지도 모른다. 그렇지만 자연은 우리에게 ‘다체 문제의 일반해’라는 선명한 눈을 허락하지 않았다. 즉, 우리는 태어날 때부터 자연을 선명하게 볼 수 없는 나쁜 눈을 가지고 태어난 것이다. 따라서 우리는 시력을 교정해야 했고, 밀도범함수이론이 교정의 역할을 훌륭하게 해내고 있다. 그렇지만, 밀도범함수이론은 아직 완벽하지 않으며, 특정 물리량에 대해서는 부정확한 예측값을 제공하기도 한다. 따라서 앞으로 꾸준한 연구를 통하여 안경의 도수를 높이고, 안경의 왜곡된 부분을 줄여가야 한다. 밀도범함수이론이라는 안경이 우리의 눈에 딱 맞게 되어서, 자연이 우리에게 조금 왜곡되었지만 선명한 모습을 보여줄 수 있기를 기대한다.
 
Reference
 
[1] Hohenberg, Pierre, and Walter Kohn. "Inhomogeneous electron gas." Physical review 136.3B (1964): B864.
 
[2] Exchange-correlation potential with correct asymptotic behavior. R. van Leeuwen and E. J. Baerends. Phys. Rev. A 49, 2421 (1994).
 
[3] Kohn, Walter, and Lu Jeu Sham. "Self-consistent equations including exchange and correlation effects." Physical review 140.4A (1965): A1133.
 
[4] Perdew, John P., Kieron Burke, and Matthias Ernzerhof. "Generalized gradient approximation made simple." Physical review letters 77.18 (1996): 3865.
 
[5] Lee, Chengteh, Weitao Yang, and Robert G. Parr. "Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density." Physical review B 37.2 (1988): 785.
 
[6] Tao, Jianmin, et al. "Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids." Physical Review Letters 91.14 (2003): 146401.
 
[7] Sun, Jianwei, Adrienn Ruzsinszky, and John P. Perdew. "Strongly constrained and appropriately normed semilocal density functional." Physical review letters 115.3 (2015): 036402.

[8] Schauer, Volker, and Christian Linder. "All-electron Kohn–Sham density functional theory on hierarchic finite element spaces." Journal of Computational Physics 250 (2013): 644-664.
 

자연과학대학 홍보기자단 자:몽 유경민 기자 yukm0227@snu.ac.kr
카드뉴스는 자:몽 인스타그램 @grapefruit_snucns에서 확인할 수 있습니다.