자연대 홍보기자단 자:몽 7기 | 이시아

[연구, 어떻게 하지?]에서 네 번째로 취재한 연구원은 CFD(Computational Fluid Dynamics) 분야의 한 연구원이다. 연구는 그에게 ‘어두운 미로 속에서 끝없이 길을 찾는 느낌’을 준다고 한다. CFD 연구원으로서 ‘연구는 어떻게 하는가?’ 그리고  ‘연구자로서의 삶은 어떠한가?’ 에 대한 이야기를 들어보자.

Q. CFD(Computational Fluid Dynamics)란 무엇인가요?

A. 유체의 흐름을 나타내는 편미분 방정식을 차분하여 컴퓨터로 풀어내는 방법을 지칭합니다. CFD 연구는 유체와 관련된 편미분 방정식의 수치적 해법을 개발하는 것과 유체 흐름을 응용하는 연구로 크게 나눌 수 있습니다. 전자의 경우는 수치해법의 정확도 및 수치해의 안정성을 향상하는 연구에 중점을 두며, 후자의 경우는 유체의 흐름이 수반되는 자연현상 및 공학 분야의 연구에 중점을 두는데 기상학, 해양학, 천문우주, 기계 분야, 자동차 및 우주항공 분야 등이 있습니다.

Q. ‘유체의 흐름을 나타내는 편미분 방정식’에 대해 설명해주세요.

 
 A. 유체는 일정한 형태가 없으며 입자 간의 상호작용을 통해서 흐름이 나타나는데 이를 해석하기 위해서는 유체의 물리적 법칙을 기술한 방정식의 해를 구해야 합니다. 나비에-스톡스 방정식(Navier-Stokes Equations)은 유체의 흐름을 나타내는 대표적인 방정식인데 실제 문제에서는 물리적인 조건이 추가되거나 완화됨에 따라 방정식을 다양한 형태로 변형하여 해를 구합니다. 예를 들어 적은 압력 범위에서 작용하는 액체의 경우에는 유체가 가진 압축성이 매우 작아지며 이 경우에는 비압축성 형태로 변형하여 문제를 해석합니다. 또한 점성의 영향이 크지 않거나 무시할 정도로 작은 경우에는 점성항을 제거한 오일러 방정식(Euler Equations)으로 변형하여 문제를 해석하기도 합니다.

Q. 해석적 방법과 수치적 방법의 차이는 무엇인가요?

 A. 유체의 흐름은 질량, 운동량, 에너지 보존을 나타내는 편미분 방정식으로 기술되는데 몇몇 특정한 상황에서는 해석적인 해가 존재하는 경우도 있습니다. 하지만 일반적인 초기조건과 경계조건에서는 해석적인 해가 알려지지 않았습니다. 그래서 풀이의 대상이 되는 영역을 격자계로 분할하고 미분 방정식을 차분 방정식으로 변형하여 대수 방정식의 형태로 문제를 해석하는 수치적인 접근이 주로 사용됩니다. 해석적인 해를 모르는 상황에서 수치적인 해법은 유일한 접근법이지만 높은 정확도로 해를 구하기 위해서는 세밀한 격자계가 필요하며 많은 대수 방정식을 풀어내기 위해 많은 수치 연산이 필요합니다.

Q. CFD 분야에서 컴퓨터의 역할은 무엇인가요? CFD 연구를 수행하는데 요구되는 컴퓨터의 성능은 어떠한가요?
 

 A. 격자계에는 매우 많은 격자점이 있으며 하나의 격자점마다 유체의 흐름을 나타내는 변수들이 지정됩니다. 모든 격자점의 변수들을 모아 행렬을 구성하여 대수 방정식을 풀어야 하므로 컴퓨터 없이는 연구의 진행이 불가능합니다. 컴퓨터의 성능이 높을수록 더 짧은 시간 내에 결과를 얻을 수 있기 때문에 CFD 응용은 컴퓨팅 기술과 밀접한 관계가 있습니다. CPU의 속도가 빨라지고 멀티코어 기술이 발달함에 따라 과거에 슈퍼컴퓨터가 필요했던 문제를 현재는 데스크탑으로도 해결할 수 있습니다. 컴퓨터가 빨라진 만큼 더 손쉽게 높은 정확도로 해를 구할 수 있게 되었지만, 그만큼 학계에서 요구하는 기대치가 높아지고 있습니다. 다만 컴퓨터는 문제를 풀어내는 도구에 불과합니다. 더 빠른 새 컴퓨터를 구입한 것이 곧 연구 업적이라 인정받는 경우는 없겠지요. 많은 연구자는 동일한 계산으로 더 정확한 해를 얻기 위한 이론적인 연구를 계속하고 있습니다.

Q. CFD 분야의 연구 주제에 대해서 더 자세히 알고 싶습니다.
 

 A. 엄밀한 서술은 아니지만, CFD와 관련한 이론적인 연구는 복잡한 유체 현상의 해를 더 정확하고 빠르게 구하는 것이라 봐도 됩니다. 현재까지도 쉽게 해를 구할 수 없는 유체역학 문제가 많으며 그중에서 우리 생활에 가장 중요한 것은 난류 유동과 관계된 해를 얻는 것입니다. 점성이 있는 유체는 작은 소용돌이를 일으키며 운동량과 에너지를 전달하는데 이런 현상을 난류 유동이라고 부르며 우리 주위의 바람, 강물 등의 흐름에서 흔히 볼 수 있습니다. 우리가 살고 있는 대기와 바다의 흐름은 난류 유동이며 자동차, 선박, 항공기 등의 공학 분야에서도 난류 유동이 대부분을 차지하고 있습니다. 하지만 작은 난류 소용돌이를 해석하기 위해서는 매우 세밀한 격자계가 필요하며 많은 계산이 요구되기 때문에 근사적인 해를 얻는 데 그치고 있습니다.

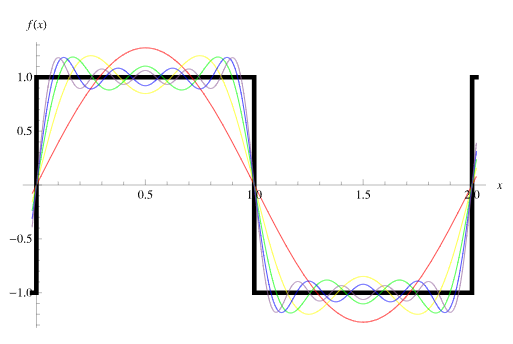
Gibbs 현상. (사진 = Weisstein, Eric W. "Gibbs Phenomenon." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/GibbsPhenomenon.html)

 또 다른 연구 주제로는 불연속면의 해석을 들 수 있습니다. 유체에는 압력 및 밀도가 급격하게 변하는 지점이 있을 수 있습니다. 대표적으로 초음속 항공기가 비행할 때나 강력한 폭발 현상이 있을 때 충격파가 발생하는데, 충격파의 전후로 압력이 급격하게 변하므로 사람이 충격파를 만나면 강렬한 폭발음을 듣게 됩니다. 충격파를 비롯한 불연속면은 수학적으로 미분 불가능한 지점에 해당하므로 밀도나 압력의 미분값을 구할 수 없습니다. 수치적인 해법을 이용하면 불연속 함수를 연속함수로 근사하는 과정에서 오차가 발생하는데, 불연속 지점 근처에서 실제 유동 현상이 아닌 진동 현상(Gibbs 현상)이 수치적으로 나타납니다. 그런데 진동 현상을 억제하는 수학적 방법을 추가하면 불연속면이 제대로 표현되지 않거나 작은 소용돌이가 소산되어 사라지는 현상이 나타납니다. 그래서 불연속면의 급격한 기울기를 잘 표현하면서도 진동 현상을 억제하는 수학적 방법이 필요합니다.

Q. 그러한 수치 해법(numerical scheme)을 개발하는 것이 CFD의 연구라고 하는데 무엇을 의미하나요? 그리고 구체적인 연구 과정에 대해 설명해 주세요.
 

 A. 이해하기 쉽게 설명하자면, 미분 방정식을 차분 방정식으로 변환해서 풀어내는 수학적인 절차를 numerical scheme이라고 합니다. CFD 분야에서는 예측되는 해의 형태를 고려하여 유체 문제의 편미분 방정식을 차분 방정식으로 변환합니다. 구하려는 해가 난류의 영향을 많이 받는지 또는 불연속을 포함하는지의 여부에 따라 각각 다른 방법으로 차분 변환을 합니다. 따라서 다양한 numerical scheme이 있으며 더 넓은 범위의 유체 문제에서 효율적으로 해를 구할 수 있도록 개선하려는 연구를 지속하고 있습니다.
 연속이며 미분 가능한 함수의 근삿값은 테일러 전개를 통해 쉽게 얻을 수 있으며 여러 번 미분 가능한 함수라면 더 정확한 결과를 얻을 수 있습니다. 하지만 불연속이 포함된 해가 예상되는 경우는 이런 단순한 방법이 통하지 않습니다. 구하려는 해의 정확한 형태를 알 수 없는 상황인데, 연속으로 추정되는 경우에는 테일러 전개의 정확도를 가지고, 불연속 근처로 추정되는 경우에는 더 낮은 정확도이긴 하지만 Gibbs 현상이 없는 수학적인 근사식을 구성해 나가는 과정이 필요합니다. 가장 기본적으로는 특정 지점의 중앙을 비롯한 좌측과 우측의 기울기 변화가 얼마나 급격하게 일어나는지를 비교해서 불연속의 근사 또는 연속함수의 근사를 사용하는 방법이 현대적인 numerical scheme의 근간이 되고 있습니다. 이런 방법은 불연속면의 진동을 억제할 수 있지만 좌, 우측의 정확도가 낮아지는 단점이 있어서 최근에는 불연속면 인근의 연속구간의 정확도를 높이는 연구가 계속되고 있습니다.

Q. 연구하시면서 어려운 문제는 무엇인가요? 그리고 이런 문제를 어떻게 해결하시나요?

A. 지금까지의 numerical scheme 개발자들이 겪는 가장 큰 문제는 기울기가 큰 연속함수를 불연속면과 구분하기 쉽지 않다는 것입니다. 이미 해석적인 수식을 알고 있는 함수라면 연속과 불연속을 구분하는 것이 매우 쉽지만, 정답을 모르는 미분 방정식의 해를 근사하는 상황에서는 연속과 불연속의 구분이 매우 모호합니다. 그 때문에 불연속이 예상되는 부분 역시 기울기가 큰 연속함수로 근사하는 방법을 사용하고 있지만 이런 상황에서도 Gibbs 현상이 나타날 수 있어서 다양한 수학적 방법을 고안하고 있습니다. 최근에는 인공지능 분야에서 널리 사용되는 딥러닝 방법을 이용한 연속과 불연속의 구분 및 CFD 응용도 시도하고 있는데, 부분적으로 의미 있는 결과를 얻기도 하지만 아직 기존의 numerical scheme을 대체하지는 못하고 있습니다.

Q. CFD 분야의 연구는 다른 연구자나 연구 그룹과의 협업이 중요한가요? 만약 그렇다면 어떤 방식으로 협력하시나요?

A. 앞서 말씀드린 것처럼 더 좋은 해를 구할 수 있는 numerical scheme을 구성하는 방법을 찾아야 하는데, 기존의 아이디어만 참고해서는 한계가 있습니다. 다른 연구자들과 토론을 통해서 새로운 아이디어를 얻거나 다른 분야 연구자들의 수학적 기법에서 단서를 얻기도 합니다. 또한 인공지능 분야처럼 전혀 새로운 부분에서 돌파구를 찾으려는 시도 역시 계속하고 있습니다. 세상의 모든 연구가 그렇듯 혼자만의 힘으로 거대한 탑을 쌓을 수 없습니다. 이미 알려진 지식의 탑 위에 작은 돌을 하나 올려놓는 것과 같은 일을 여러 사람과 함께 할 뿐입니다. 최근에는 IT 기술의 발달 덕분에 더 편리하게 컴퓨팅할 수 있으며 깃허브(Git Hub) 등의 공유 인프라가 발달해 연구자들이 서로의 코드와 아이디어를 더 쉽게 주고받을 수 있게 되어 연구에 도움이 되고 있습니다.

Q. 일과를 알려주실 수 있으신가요? 정해진 출퇴근 시간이 있나요?

A. 연구원으로서의 최소 근무 시간 규정이 있습니다만 대부분의 연구자가 그렇듯 연구 관련 생각이 항상 마음 속에 있습니다. 저의 경우는 수식을 써보고 컴퓨터로 옮겨 코드를 작성하는 것이 가장 중요한 일과입니다. 차분 방법을 다르게 전개해 보고 그 결과를 컴퓨터로 계산해 본 다음 다시 개선하는 작업을 지속하다가 관련 논문을 찾고 읽어보며 아이디어를 얻는 일을 반복하고 있습니다. 근무시간 중에 여러 가지 아이디어를 얻기 위해서 토론하다가 좋은 아이디어가 떠오를 때는 그 생각을 놓치지 않기 위해서 늦은 밤에도 일을 하는 식이라 정해진 근무 시간을 채우는 것이 의미를 갖지는 않는 것 같습니다.

Q. 내가 생각하기에 연구는 ________다. 빈칸에 들어갈 말을 채워주세요.

A. 저에게 연구는 ‘어두운 미로 속에서 끝없이 길을 찾는 느낌’을 줍니다. 저 멀리 작은 빛이 보이지만 얼마나 더 가야 끝인지 알 수 없습니다. 연구에 작은 단서를 찾으면 출구가 더 가까워진 것 같아서 보람을 느끼지만, 그것이 해결 방법이 아님을 알게 되면 다시 새로운 난관이 다가오기도 합니다. 복잡한 유동을 잘 표현하는 근사함수가 불연속 근처에서 Gibbs 현상을 유발하는 문제가 생기는 것처럼요. 가끔은 오랜 시간을 투입한 아이디어가 쓸모없는 것으로 판단되는 경우도 있습니다. 연구가 답보상태에 있을 때 다른 연구 분야에 뛰어들어 볼 마음이 생기기도 합니다. 하지만 해당 분야 연구원들도 비슷한 어려움을 겪고 있겠지요. 그런데 연구원이 꼭 한 가지 연구만 하라는 법은 없는 것 같습니다. 자신이 열정을 다 할 수 있는 분야라면 그 어떤 분야의 연구도 할 수 있으니까요.

지금까지 한 CFD 분야 연구원의 연구방법과 연구자로서의 삶에 대한 이야기를 들어보았다. 이 이야기가 CFD 분야 전체를 대변할 수는 없겠지만, 정해진 시간 외에도 늘 연구를 생각한다는 그의 말에서 연구자가 가져야 할 중요한 자질을 배울 수 있었다. 지금 이 순간에도 ‘어두운 미로 속’에서 길을 찾기 위해 고군분투하며, 더 나은 연구를 향해  끊임없이 도전하는 모든 연구원들의 노력에 경의를 표한다.

참고 자료

https://mba-consultants.co.uk/computational-fluid-dynamics-modelling-in-house/
 Weisstein, Eric W. "Gibbs Phenomenon." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/GibbsPhenomenon.html

자연과학대학 홍보기자단 자:몽 이시아 기자 siasia7788@snu.ac.kr
카드뉴스는 자:몽 인스타그램 @grapefruit_snucns에서 확인할 수 있습니다.