자연대 홍보기자단 자:몽 7기 | 송주형

* 소속: 통계학과
* 연구분야: 불확실성 계량화, 환경 및 의생명과학을 위한 기계학습
* E-mail: wonchang@snu.ac.kr
* Tel: 880-4251

작년 9월, 서울대학교 통계학과에 새로 부임하신 장원 교수님을 인터뷰했다. 교수님께서는 통계학과에 계시지만 기후과학, 의생명과학 등 다른 분야에 대한 연구도 많이 하셨다. 통계학을 이용하여 다양한 분야에 숨겨져 있는 불확실성을 찾아내고 이를 정량화하여, 우리가 더 과학적인 과학을 할 수 있도록 도움을 주고 계신 교수님의 이야기를 들어보자.

 
 
 1. 작년에 새로 부임하신 만큼 아직 교수님에 대해 잘 모르는 학생들이 많을 것 같습니다. 학생들을 위해 교수님에 대한 간단한 소개 부탁드립니다.

저는 미국에서 15년간 살면서 교수로 8년 동안 재직하였고, 9월 1일에 서울대학교 통계학과로 부임하였습니다. 제가 국적 때문에 학교 홈페이지에는 이름이 영어로 Won Chang이라고 되어 있을 텐데 한국 이름은 장원입니다(웃음). 고려대학교 통계학과에서 학사와 석사를 하고, 박사는 펜실베니아 주립대학교에서 마쳤습니다. 그 이후 시카고 대학교에서 포닥을 한 다음 신시내티 대학교에서 8년간 교수로 있다가 기회가 되어 서울대학교 통계학과로 오게 되었네요. 연구 관련 얘기는 추후에 이어서 하겠지만, 머신러닝이나 여러 통계적인 방법론을 이용해서 기후과학, 생명과학 등 다양한 분야에 응용하는 연구를 많이 하고 있습니다.
ㅤ

2. 서울대학교의 신임 교수님이 되신 소감이 궁금합니다.

그동안 미국에서 쭉 사는 동안 한국에 오고 싶다는 마음이 들었는데 마침 서울대학교에 부임하게 되어 굉장히 행운이라고 생각합니다. 서울대에 와보니 학생들이 확실히 열의가 많아서 정말 좋은 것 같습니다(웃음).

3. 교수님의 연구 분야와 앞으로 이곳에서 펼쳐 나가실 연구에 대한 소개 부탁드립니다.

제가 주로 연구하는 것에 대해서 저는 보통 2가지를 얘기하는데, 하나가 Uncertainty quantification(불확실성 계량화)이라고 하는 분야입니다. 다만 단어가 조금 모호해서 많은 혼란을 불러일으키는데, 실제 통계학에서 불확실성 계량화의 의미는 모델 시뮬레이션을 할 때 관계된 불확실성들을 통계적인 방법으로 더 정밀하게 분석을 하는 것을 말합니다. 특히나 기후, 기상 시뮬레이션 모델들을 사용할 때 여러 가지 불확실성들이 내재되어 있어요. 제일 대표적인 것이 parameter uncertainty(파라미터 불확실성)입니다. 기후과학 분야에서는 parameter를 ‘매개변수’라고 하고 통계학에서는 ‘모수’라고 부르죠. 를 잘 정하지 않으면 시뮬레이션이 현실을 잘 반영하지 않을 수 있습니다. 그 외에도 모델에 내재된 구조 자체가 실제 자연 현상과 차이가 있기 마련인데, 이를 '모델 구조에 대한 불확실성'이라고 합니다. 같은 현상을 분석할 때에도 여러 가지 후보 모형들을 놓고 하는데, 이들 중 뭐가 맞는가를 따질 때 관계된 불확실성이죠. 근데 모델 구조에 대한 불확실성이 파라미터 불확실성이랑 같이 엮여있기도 합니다. 모델이 안 맞는 이유는 파라미터 혹은 구조가 안 맞기 때문일 수 있는데 그 둘이 엮여있을 수도 있다는 거죠.
보통 불확실성 계량화를 할 때 관측 데이터랑 시뮬레이션이 주는 결과가 시공간 데이터인 경우가 대부분입니다. 특히 지구환경과학 데이터들이 전부 시공간 데이터들이거든요. 그래서 제 연구분야는 불확실성 계량화이지만 그걸 잘하기 위해서 박사 때 시공간 데이터 분석(spatiotemporal data analysis) 공부도 많이 했습니다.

3-1) 나머지 한 분야는 기계학습 연구인가요?

일단 앞서 말한 불확실성 계량화를 하려면 기계학습 모형의 도움을 받아야 하는 경우가 많습니다. 왜냐하면 결국 빅 데이터를 다루어야 하기 때문입니다. 엄청나게 복잡한 컴퓨터 시뮬레이션에서 나온 결과와 엄청나게 복잡한 현실 데이터를 연결해야 하는데, 이를 잘 할 수 있는 모형이 기계학습 모형들입니다. 그래서 저도 최근에는 기계학습 모형을 많이 사용하고 있습니다. 근데 여기서 재밌는 점이, 기계학습 분야 내에도 불확실성 계량화라는 연구 주제가 있습니다. 이건 앞서 설명한 불확실성 계량화하고 비슷하면서도 다른데, 기계학습 모형 자체에 대한 불확실성을 연구하는 겁니다. 처음에 기계학습 혹은 딥러닝 모형들이 등장했을 때에는 통계 쪽 분야의 사람들이 많이 관여되어 있지 않았습니다. 그래서 초창기에 다른 분야에서 연구하시는 분들이 기계학습 모형을 많이 사용했을 때에는 AI나 기계학습 모형들을 사용할 때 나오는 불확실성에 대한 관점이나 생각이 별로 없었어요. 그러다가 시간이 점점 지나면서 통계학자들을 포함한 다양한 분야의 사람들이 머신러닝 등 AI 쪽 연구를 하게 되었습니다. 통계학의 요체가 결국 예측을 하나 하더라도 얼마나 이 예측이 확실한지를 정량적으로 제시하는 건데, 통계학자 분들이 기계학습 모형에 대해서 그런 작업들을 하기 시작한거죠. 제가 앞서 설명한 불확실성 계량화랑 기계학습에서의 불확실성 계량화는 닮은 부분이 많고, 공통된 테크닉을 사용하는 경우도 있어서 요즘은 기계학습에서의 불확실성 계량화에 흥미가 생겨 그쪽을 연구하려고 합니다.

불확실성 계량화의 핵심에 대해 예를 들어서 다시 설명하자면, 물리 기반 시뮬레이션을 이용해서 기후를 컴퓨터로 시뮬레이션할 때 확률 편미분 방정식¹(Stochastic partial differential equations, SPDEs)로도 할 수 있겠죠. 근데 잘 안 합니다. 보통 그냥 편미분 방정식(Partial differential equations, PDE)으로 합니다. 왜 그럴까요? 너무 복잡하고 안정화도 안 되고 오차항(Error term)을 조금만 바꾸면 결과가 막 난리가 나거든요. 저는 기후학자들과 오래 일해봐서 그 어려움을 잘 아는데, PDE 모형으로 해도 실제 지구와 비슷한 시뮬레이션을 만드는 게 정말 힘든 작업입니다. 근데 그런 불확실성을 고려하지 않은 모형에서 불확실성을 끌어내서 우리가 얼마나 아는지 혹은 모르는지에 대한 불확실성 경계(혹은 범위)를 제시하고 싶은 게 결국 불확실성 계량화의 핵심입니다. AI 모델에서의 불확실성 계량화도 비슷한 점이 많아서 그쪽도 파려고 하는 중에 있는 거고요.

1) 확률 편미분 방정식: 확률 과정이 포함되어 있어 불확실성이 들어간 편미분 방정식이다. 클라우스 하셀만(Klaus Hasselmann)은 1976년 확률적 대기 강제력이 포함된 기후 모형을 제안하였고, 2021년 노벨 물리학상을 수상했다.
ㅤ

3-2) 그렇다면 기후 모형을 AI 모델로 대체하자는 건가요?

그런 질문을 종종 받는데 아직까지 그 정도는 아니라고 봅니다. 만약 AI를 그런 방식으로 사용한다고 하면 그나마 제일 현실적인 게 거대한 기후 모형 속 어떤 부분만 골라서 그 부분에 대한 연산 속도를 빠르게 하기 위해 AI 모델로 대체를 하는 정도입니다. AI라는 게 말은 거창하지만 실제로는 그냥 경험적 모델입니다. 물리 모델을 경험적, 통계적 모델로 대체해서 속도를 빠르게 하자는 건데 통계 분야에서는 이를 emulation이라고 합니다. AI를 이용해서 일부분만 대안적으로 시뮬레이션할 수는 있지만 전체를 시뮬레이션하자는 건 아닙니다.
그래서 저는 보통 어떤 식으로 사용하려고 하냐면, 예를 들어서 최적의 파라미터(parameter) 값을 추정하고 싶다고 합시다. 어떤 파라미터 값을 기후 모형에 넣었을 때 모형에서 생산되는 결과가 있을 겁니다. 이때 input(입력변수)이 파라미터들이고 output(출력 변수)이 기후 시뮬레이션의 결과인 함수 관계를 얻어낼 수 있습니다. 이 함수 관계를 AI 모델로 학습해서 함수 관계를 비슷하게 모사하는 모델로 만드는 작업을 할 수 있고, 그 반대의 작업도 할 수 있습니다. 파라미터가 x1일 때에는 기후 모형의 결과값이 y1이고, 파라미터가 x2일 때에는 기후 모형의 결과값이 y2이고… 이런 예시를 AI 모델한테 엄청 많이 보여주고 학습을 시킨 후에 현실 데이터 X를 가지고 와서 AI 모델한테 X에 가장 적합한 파라미터 값 Y는 얼마인지 추정하게 하는 방식으로 최적의 파라미터를 추정할 수 있습니다.
ㅤ

3-3) AI를 이용해서 엘니뇨를 예측하는 연구¹들도 비슷한 원리인가요?

그런 연구들은 AI를 이용해서 과거의 데이터를 가지고 경험적, 통계적인 방법으로 목표가 되는 기후 현상을 예측하는 겁니다. 여담으로 통계학자가 이런 말을 하기에 좀 웃길 수도 있겠지만 그래도 그런 예측들을 하려면 물리적인 역학 과정이 들어간 모델을 사용하는 게 더 적절하지 않을까하는 생각이 있습니다². 그러니까 calibration과 같은 통계적인 방법을 사용해서 물리적인 역학 과정이 들어간 모델이 더 잘 작동할 수 있도록 통계학을 사용하는 게 조금 더 맞는 접근법이라고 생각합니다. 하지만 AI를 이용해서 기후 현상을 예측하는 연구들도 대단히 흥미롭게 지켜보고 있습니다.

1) 2019년 함유근 교수님 연구팀이 합성곱 신경망³을 이용해서 엘니뇨를 예측하는 모델을 만들었다(Ham et al., 2019). 당시에 존재하던 엘니뇨 예측 모델들 중 가장 예측 성능이 좋은 모델로 평가받았다.
2) 2024년 6월 국종성 교수님 연구팀이 ‘확장된 비선형 재충전 진동자 모델(Extended nonlinear recharge oscillator model, XRO model)’이라는 엘니뇨 역학 과정이 포함된 모델을 만들었는데 XRO 모델의 예측 성능이 AI 모델에 버금갈 정도로 좋다는 연구결과가 발표되었다(Zhao et al., 2024).
3) 합성곱 신경망과 딥러닝의 기틀을 다진 존 홉필드(John hopfield)와 제프리 힌튼(Geoffery Hinton)은 2024년 노벨 물리학상을 받았다.

4. 교수님께서 현재 전공 분야를 공부하시게 된 계기는 무엇인가요?

아주 짧은 답은 박사 과정 때 지도교수님이 시켜서입니다(웃음). 농담처럼 하는 말인데 사실이기도 하죠. 저는 시공간 분석이랑 베이지안 추론(Bayesian inference)에 관심이 있었습니다. 특히 전산 통계(Computational Statistics)에 관심이 있어서 박사 때 지도교수님과 만나서 그 분야를 연구하고 싶다고 얘기하니까 불확실성 계량화를 소개해주시더라고요. 당시 지도교수께서 기후과학을 연구하는 지구과학과¹ 교수님과 같이 연구하고 계셨는데 그 공동연구에 제가 참여할 수 있도록 해주셨습니다. 거기에 참여하면서 연구를 하다보니 적성에 맞더라고요. 지구과학 연구하시는 분들하고 얘기하는 것도 재밌었습니다. 나중에는 그 지구과학과 교수님께서 제 co-advisor(공동 지도교수)를 했습니다. 그래서 저는 지도교수가 두 명이었어요. 통계학과에 한 명, 지구과학과에 한 명. 저는 통계학뿐만 아니라 지구과학 저널에도 논문을 투고합니다. 얼마 전에 제출한 논문도 지구과학 논문이었고요. 저처럼 통계학자인데 지구과학을 연구하는 연구자들이 미국에는 좀 있습니다. 
 아마 한국 내에서 저만큼 아예 제1저자, 교신저자로 지구과학 논문을 쓰는 동시에 통계학자인 사람은 별로 없을 거에요. 근데 미국에서는 그런 분들이 꽤 있기 때문에 미국에 있는 동안에는 제가 그렇게 신기한 존재라는 생각은 안했습니다.

1) 펜실베니아 주립대 지구과학과(PennState Department of Geosciences)

5. 교수님께서 기후 모델, 특히 빙상 모델의 캘리브레이션(calibration)에 대한 연구를 많이 하신 것으로 알고 있습니다. 빙상 모델 캘리브레이션 연구를 하게 된 배경에 대해서 자세히 설명해주실 수 있으신가요?

모델 캘리브레이션(Model calibration)을 진짜 원시적으로 한다면 그냥 그림이나 자료를 보고 일일이 파라미터를 수정하는 방식으로 할 수도 있어요. 근데 그러다보니 빙상 모델 분야 연구자들이 한번 모인 적이 있었대요. 여러 집단에서 개발한 빙상 모델들을 모아서 미래를 예측한 결과를 봤는데 현재의 상황은 모델들이 다 비슷하게 모의하는 반면(손으로 하든 어떻게든 다 calibration을 했으니까) 미래를 예측한 결과는 발산하더라는 겁니다. 모델들이 미래를 다 다르게 예측해버리는 상황인 거죠. 근데 그럴 수가 없는 게 모델에 쓰인 물리적 과정들은 아주 다른 게 아니고 다 비슷비슷합니다. 아무리 다른 사람이 만들었다고 하더라도 비슷한 원리로 만들어졌는데 그렇게까지 다를 수가 없단 말이죠. 아니면 최소한 비슷한 가정을 한 모델들은 예측 결과가 비슷하게 가야하는데 그것도 아닌 거예요. 그래서 연구자들 사이에서 파라미터 불확실성을 놓친 것 같다는 의견이 나왔고, 빙상 모델 분야에서 이를 제대로 정량화 하려는 연구들을 제가 박사과정을 밟던 시기에 많이 했습니다. 결론적으로 파라미터 불확실성과 관련된 부분은 현재 많이 개선되었습니다. 통계적인 방법이 많이 도입되고 통계학자들과 빙하학을 연구하시는 분들이 잘 협업을 한 덕분이죠.
ㅤ

5-1) 모델 캘리브레이션 연구의 과정이 궁금합니다.

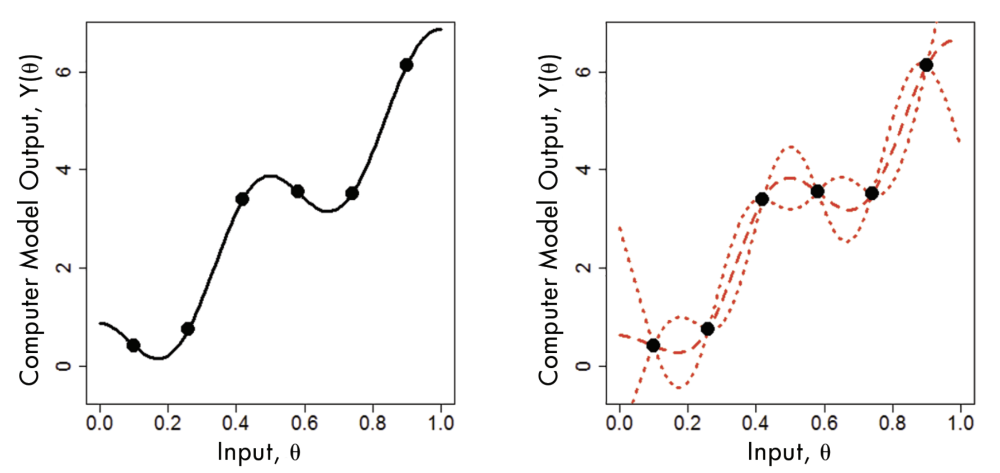
그림 1. Emulation 과정을 보여주는 그림이다. (출처 = Haran et al., 2017)

조금 다른 주제이긴 하지만 calibration을 할 때 먼저 해야 하는 건 emulation입니다. 모델 하나하나가 비싸고 컴퓨팅을 할 때 시간이 많이 걸립니다. 짧게는 30분에서 길게는 몇 시간씩,  그것도 그냥 일반 컴퓨터에서 돌리는 게 아니라 슈퍼컴퓨터에서 그 정도의 시간이 걸립니다. 그러다보니 컴퓨터 모델의 outcome(결과)이 제한된 input(입력변수)에 대해서만 존재합니다. 모든 입력변수에 대한 컴퓨터 모델의 실제 결과를 알 수 없는 거죠. 그림 1에서 underlying model(기저 모델)이 검은색 실선이라고 한다면 우리가 알고 있는 건 검은색 점들 밖에 없습니다. 그래서 그걸 먼저 interpolation(내삽)을 해줘야 합니다. 이 부분에서 머신러닝 기법이 쓰일 수 있다고 생각하면 됩니다. 보통은 내삽하는 방법으로 Gaussian process(가우시안 과정)를 쓰는데(그림 1에서 빨간색 실선이 가우시안 과정을 사용해서 내삽한 것이다) 요즘에는 딥러닝으로 해본다든가 딥러닝과 Gaussian process를 결합해서 해보는 등의 연구도 진행되고 있습니다.

 그리고 그림 1에서는 입력변수와 결과값이 1차원이니까 쉽지만 실제로는 검은색 점 하나하나가 복잡할 수도 있습니다. 검은색 점 하나하나가 고차원의 시공간 데이터일 수도 있기 때문에 그런 경우에는 어떻게 할 것인가 등의 문제를 연구하는 거죠.

 요약하자면 복잡한 물리적 모델을 모든 파라미터 조합에 대해서 돌릴 수 없고, 입력변수가 제한되어 있으니까 statistical surrogate 혹은 emulator를 이용해서 통계적으로 근사하는 걸 emulation 문제라고 합니다.

 Emulation을 하고 난 이후에 calibration을 하게 되는데 가끔은 emulation이 필요 없는 경우도 있습니다. 원래의 함수를 아는 경우에는 emulation이 필요없습니다. emulation이 필요 없는 경우와 emulation을 하고 난 경우 모두에 대해서 observation data(관측 데이터)가 주어졌을 때 어떤 파라미터가 이 관측 데이터랑 잘 맞는 좋은 파라미터인지를 추정하는 게 calibration problem입니다. 현상을 관측한 후 관측 데이터와 맞는 파라미터를 역으로 추정하기 때문에 물리학에서는 inverse problem(역문제)이라고도 하죠.

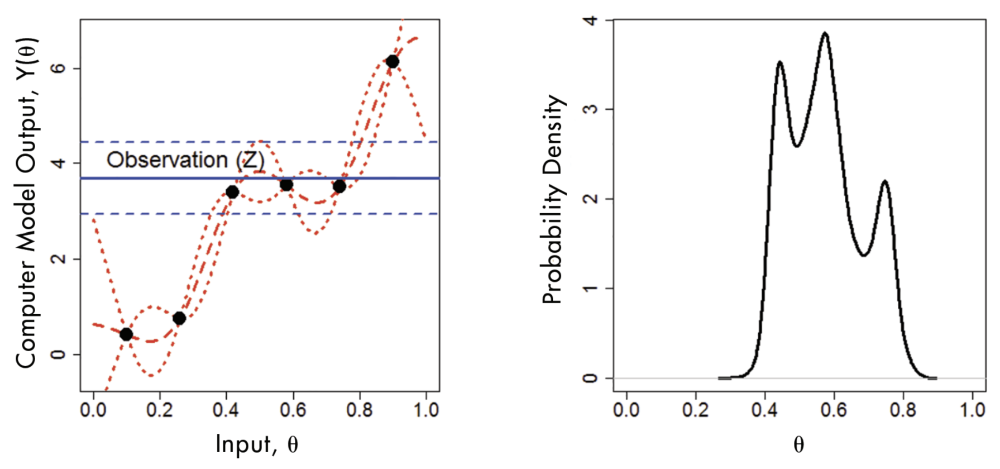
그림 2. Calibration 과정을 보여주는 그림이다. (출처 = Haran et al., 2017)

그림 2에서 파란색 선은 관측 데이터를 나타냅니다. 여기서 Bayesian inference(베이지안 추론)을 하면 오른쪽의 파라미터에 대한 posterior density(사후 분포)가 나오게 됩니다. 왼쪽 그래프에서 파란색 점선 범위 내에 존재하는 3개의 점과 오른쪽 그래프에 나타나는 3개의 극값이 서로 대응된다는 것을 알 수 있습니다. 여기서 통계적으로 calibration을 했을 때의 장점을 알 수 있는데, 가능한 파라미터 최적값의 조합들을 다 알 수 있다는 것입니다. 최적값을 하나만 찾는 것도 할 수는 있지만 그러면 모든 스토리를 알 수가 없죠. 그래서 아까 말한 빙상 모델마다 예측값이 다 달랐던 사례도 모델마다 서로 다른 파라미터 최적값을 사용해서 그런 것일 수 있습니다. Calibration을 해서 얻은 파라미터의 분포를 가지고 예측하면 그 결과가 하나의 값으로 나오는 게 아니라 어떤 범위를 가지는 prediction band의 형태로 나오는 거죠. 그러면 전체적으로 얼마나 불확실한지에 대한 정보를 다 끄집어낼 수 있는 겁니다.  따라서 이렇게 해야 더 과학적이지 않나 생각하고 있고, 모델을 잘 만드는 것도 중요하지만 parameter에 대해서 calibration을 하는 것도 중요하다고 생각합니다.

5-2) 그림 3은 어떤 그래프인가요?

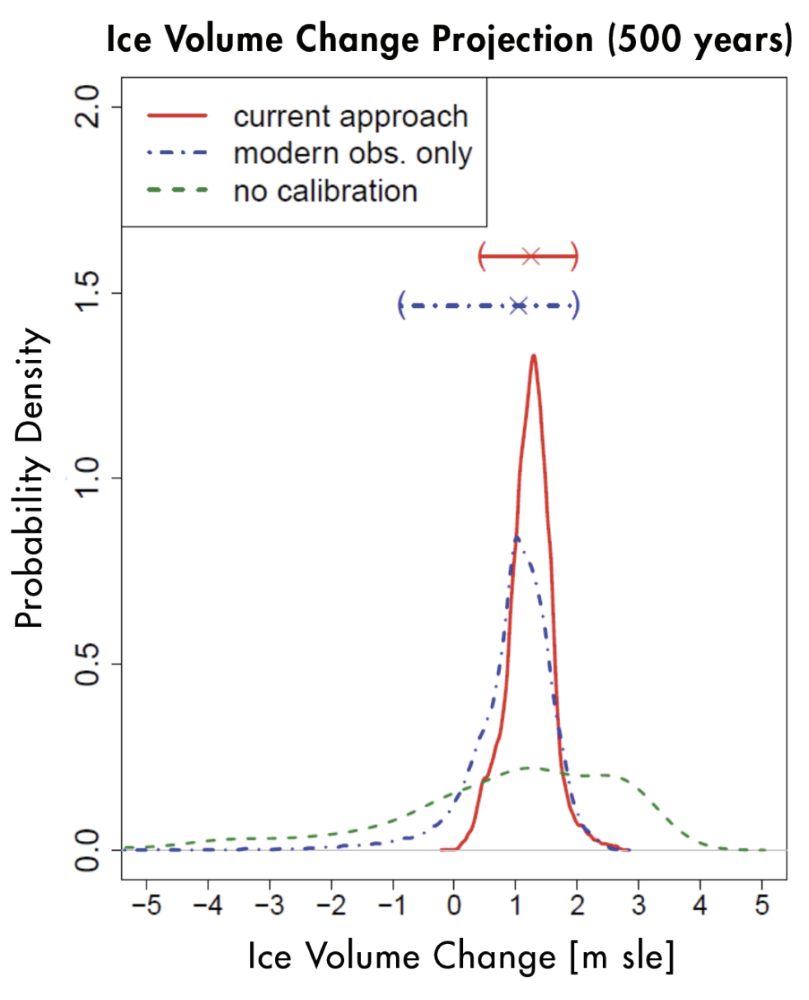
그림 3. 남극 빙하 변화량에 대한 사후 예측 분포이다. 가로축은 남극 빙하의 변화량을 해수면 상승 기여도로 환산한 것이다. 즉, 가로축에서 0보다 큰 범위는 남극 빙하가 녹아서 해수면이 상승하는 것을 의미하고, 0보다 작은 음수의 범위는 남극 빙하가 증가해서 해수면이 낮아지는 것을 의미한다.
(출처 = Haran et al., 2017)
ㅤ

이 그래프는 빙상 모델을 calibration을 한 후에 미래 빙하의 변화량을 예측한 결과를 보여주는 그래프입니다. 파란색 점선 그래프는 현재 빙상의 데이터만을 가지고 calibration을 해서 파라미터를 추정한 후 빙하의 변화를 예측한 결과입니다. 빨간색 실선 그래프는 고기후 자료(paleo record)까지 포함해서 calibration을 하고 파라미터를 추정해서 빙하의 변화를 예측한 결과입니다. 고기후 자료도 불완전하지만 정보가 들어있기 때문에 parameter uncertainty를 줄일 수 있고 예측을 더 정교하게 할 수 있습니다. 파란색(&초록색) 그래프와 빨간색 그래프를 비교해보면 빨간색 그래프는 양수의 범위에서만 존재한다는 것을 알 수 있습니다. 즉, 남극의 빙하가 미래에 늘어날 가능성을 날릴 수 있게 된 거죠. 과학적으로 흥미로운 결과였습니다.
초록색 점선 그래프는 calibration을 하지 않은 경우인데 calibration을 하지 않았다는 것은 parameter 값을 가능한 범위에서 다 똑같이 뽑아서 미래 예측을 한 것입니다. 모든 parameter 값들을 동등하게 가능하다고 보고 시뮬레이션을 하면 이렇게 된다는 거죠. 그래프를 보면 초록색은 음수의 범위에서도 존재하는데 어떤 모델은 지구온난화가 진행됨에 따라서 남극 빙하가 오히려 늘어날 것이라고 예측한 겁니다.  2010년 이전에는 남극에 눈이 많이 내려서 남극 빙하의 양이 늘어나거나 최소한 변하지는 않을 것이라는 학설이 있었습니다. 근데 이처럼 모델 calibration 연구가 진행되면서 남극 빙하의 양이 늘어날 일은 없다는 쪽으로 결론이 났습니다. 이제는 논의가 얼마나 줄어들 것이냐로 넘어갔죠.

6. AMOC¹ 예측과 관련된 연구도 진행한 것으로 알고 있습니다. 구체적으로 어떤 연구였는지 소개해주실 수 있으신가요?

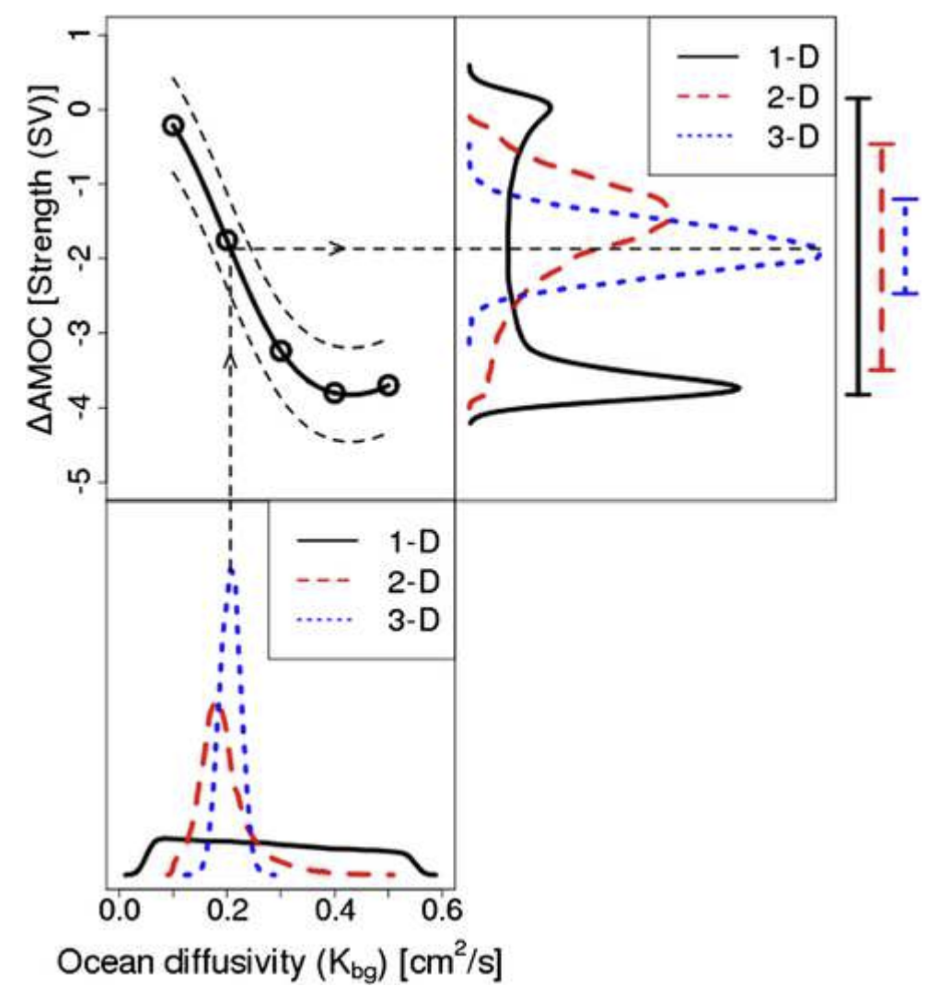
그림 4. 1-D, 2-D, 3-D 데이터에 대한 각각의 Ocean diffusivity(해양 확산 계수)의 사후 분포와 그에 따른 예측된 AMOC strength(AMOC 강도)²의 변화량 분포 그래프이다. (출처 = Chang et al., 2014)
ㅤ

얼마 전에 투고한 논문도 AMOC와 관련된 논문이었습니다. 질문하신 이 AMOC 예측에 대한 연구는 박사 때 한 연구인데요, AMOC가 어떻게 움직일지를 모델링 할 때 가장 큰 불확실성을 차지하는 부분이 Vertical background diffusivity parameter(수직 배경 확산계수)³입니다. 그래서 그걸 얼마나 잘 추정하느냐에 따라서 결론이 많이 바뀝니다. 근데 기후과학을 연구하시는 분들이 연구를 할 때 단순한 방법을 쓰는 경우가 많습니다. 많은 경우에 전체 3-D(3-dimensional, 3차원) 데이터를 다루기 힘드니까 데이터를 요약해서 사용하죠. 예를 들어, 어떤 물리량에 대해서 원래는 위도, 경도, 깊이에 대한 3차원적인 데이터가 있다면 그것을 전지구적으로 위도와 경도에 대해서 다 평균을 내서 오직 깊이에 대한 1차원적인 데이터(1-D data)로 사용한다든지, 경도에 대해서만 평균을 내서(zonal average)⁴ 위도와 깊이에 대한 2차원적인 데이터(2-D data)로 사용하기도 합니다. 이 논문에서 얘기하고자 하는 것은 그런 식으로 데이터의 차원을 줄일수록 정보 손실이 커진다는 것입니다. 전체 3차원의 데이터(Full 3D data)를 다룰 수 있으면 가급적 차원을 줄이지 않는 게 좋다는 거죠. 3차원 시공간 데이터를 그대로 써서 캘리브레이션을 해야 좋은 결과가 나온다는 것을 실제로 증명했습니다. 
 그림 4에서 가장 아래에 나와있는 그래프는 각각 1-D, 2-D, 3-D 데이터를 가지고 캘리브레이션을 했을 때 ocean diffusivity paramter(해양 확산 계수)의 사후분포입니다. 왼쪽 상단에 있는 그래프는 제가 연구할 때 사용했던 모델인 UVic ESCM(University of Victoria Earth System Climate Model)모델을 통해 얻은 ocean diffusivity와 AMOC 강도 변화량의 관계입니다. 가장 아래의 해양 확산 계수 사후분포 그래프를 이용해서 왼쪽 상단 그래프의 관계에 대입하면 우측 상단에 나와있는 AMOC 강도 변화량 분포 그래프가 나옵니다. 그러니까 각각의 1-D, 2-D, 3-D 데이터에 대해서 파라미터를 추정한 후, 추정된 파라미터 분포를 가지고 AMOC 강도의 변화량을 추정하는 거죠. 결과를 보면 1-D 데이터로 추정된 AMOC 강도의 변화량과 3-D 데이터를 통해 추정한 AMOC 강도의 변화량이 아주 다르다는 것을 볼 수 있습니다. 전체 3차원 시공간 데이터를 사용하지 않고 데이터를 요약해서 차원을 줄여버리면 아예 다른 결과가 나온다는 거죠. 특히 1-D 데이터는 캘리브레이션이 거의 안된 상태라서 가능한 모든 범위 안에서 파라미터 분포가 균일하게 나온 건데 이런 식으로 정보가 불완전한 상태에서 파라미터 값을 모델에 집어넣으면 미래 예측값이 완전히 달라져버립니다.

가끔은 ‘왜 굳이 full 3D로 모든 데이터를 쓰려고 하냐, 그냥 summary statistics(요약된 통계량)⁵만 써도 되지 않냐, 너 통계학자 아니냐’라고 질문을 하는 사람들이 있어요. 근데 원래 통계학이 그런 걸 하는 학문은 아닙니다. 정보를 요약하거나 줄이는 게 아니라 사실은 반대로 가급적 모든 정보를 다 사용하려고 하는 게 통계학이거든요.

 여담으로 이 AMOC 예측 연구가 박사 때 처음 쓴 통계학 논문입니다. 통계 논문 중에 제일 처음 나온 논문이죠.

1) AMOC(Atlantic Meridional Overturning Circulation, 대서양 자오선 역전 순환): 열염 순환 혹은 컨베이어 벨트로도 알려져 있는 AMOC는 대서양에서 저위도의 따뜻한 해수가 고위도로 이동해서 고위도 지역에서 해수가 침강하는 순환이다.
2) AMOC 강도(AMOC strength): AMOC를 통해 수송되는 해수의 수송량이다. 지구온난화로 인해 AMOC의 강도가 점점 감소하고 있다.
3) Ocean diffusivity(해양 확산 계수), Vertical background diffusivity(수직 배경 확산계수): 둘은 같은 말이다. 해양에서 표층의 해수가 심층의 해수와 수직적으로 얼마나 잘 섞이는지를 나타내는 확산계수이다. AMOC는 고위도 지역에서 표층의 해수가 심층으로 침강하면서 발생하는 순환이기 때문에 표층수와 심층수의 혼합이 활발해질수록 AMOC가 강해진다. 즉, 해수의 혼합을 알려주는 확산 계수를 가지고 AMOC를 예측할 수 있다.
또한, 그림 4에서 볼 수 있듯이 AMOC에 대한 미래 예측을 했을 때 AMOC가 감소하는 양(AMOC 강도의 변화량) 또한 확산계수가 클수록 크다는 특성이 있다(Goes et al., 2010, Chang et al., 2014).
4) Zonal average: 경도에 대해서 어떤 물리량을 평균을 냈을 때 zonal average라고 한다. 위도에 대해서 평균을 내면 meridional average라고 한다. AMOC는 위도 방향(자오선 방향)으로 이루어지는 순환이기 때문에 기후과학에서 종종 zonal average를 한 물리량을 사용하기도 한다.
5) Summary statistics(요약된 통계량): 본문에 나온 1-D, 2-D 데이터와 같이 정보의 차원을 줄이거나 요약한 통계량을 의미한다.

7. 의생명과학 관련 연구도 하신 것으로 알고 있는데, 어떤 연구를 진행하셨었나요?

2022년에 제가 안식년을 하는 동안 ibs 의생명 수학 그룹¹에 방문해서 연구를 좀 했었습니다. 거기는 생명현상에 대한 ODE², PDE 등을 써서 연구를 하는, 응용수학을 하시는 분들이 계세요. 거기도 모델 캘리브레이션과 uncertainty quantification을 해야하고 유전 데이터와 같은 빅 데이터를 많이 다루어야 해서 같이 협업하여 연구했었습니다. 지금도 그분들하고 계속 연구를 하고 있습니다. 최근에는 질병 예측과 관련된 연구를 했습니다. SEIR 모델을 쓸 때 모델 피팅(model fitting)을 하면서 초기 조건을 어떻게 하면 잘 추정할 수 있는지를 연구한다든지, 확진자들의 양상을 잘 모델링하고 예측을 하려면 노출군(exposed class)³에 대한 추정이 정확하게 되어야 하는데 어떻게 하면 기존 방법보다 개선된 방법으로 잘 추정할 수 있는지 등을 연구합니다. 그러면서 동시에 uncertainty도 계량을 다 해야하죠. 그래야 과학적인 결론을 낼 수 있으니까요. 그런 부분에 제가 도움을 줬었습니다.

 유전체 데이터와 관련된 예시도 하나 소개할게요. 유전체 데이터를 다룰 때 보통 하고 싶어하는 게 세포들을 군집화(Clustering)하는 것입니다. 유전 정보에 따라서 세포들이 각각 어떤 유형의 세포인지를 군집화하고 싶어합니다. 근데 이제 그 군집화 작업을 할 때 제가 앞서 얘기했던 빙하 모델을 연구하면서 얻었던 경험이 유용하게 사용되었습니다. 빙하 모델 같은 경우 얼음이 없는 데에서는 다 두께가 0으로 처리되고 두께가 있으면 어떤 양수의 값으로 나오는 특징이 있는데 유전체 데이터도 비슷한 성질이 있습니다. Detection limit(검출 한계)보다 낮은 데에서는 다 0이란 값으로 나오고 검출 한계 위에서는 어떤 양수의 값으로 나옵니다. 그런 식으로 0이 많은 데이터를 zero-inflated data라고 합니다. 근데 그런 데이터를 다룰 때에는 특별한 통계적 고려가 많이 필요합니다. 왜냐하면 보통 우리가 만드는 통계적 방법들은 가우시안 분포와 같이 그냥 연속적이고 경계가 없는 분포를 상정하고 이론을 전개해서 만들어지기 때문입니다. 그래서 유전체 데이터와 같이 0에 딱 bound됐을 뿐만 아니라 실제로 관측된 0 값이 무지하게 많은 그런 데이터는 다르게 취급을 해야하는 거죠. 그래서 조금 웃기면서도 재밌는 게, 빙하 관련 데이터를 다루면서 이미 그런 걸 많이 봤었는데 유전학 쪽을 가니까 비슷한 종류의 데이터들이 있는 거죠.

 그리고 또 재밌는 부분이, ibs에 계신 분들도 처음에는 zero-inflate 때문에 저한테 찾아온 게 아니었어요. Dimension reduction(차원 축소)을 하는 데 자꾸 생각했던 것처럼 안되더라는 겁니다. Random matrix theory(무작위 행렬 이론)를 써가지고 dimension reduction을 하는 데 이론대로 안되니까 저한테 왔던 거였습니다. 그래서 제가 봤는데 안될 이유가 없는데..? 하고 보다가 데이터에 0이 많아서 왜 그런지 물어보니 원래 detection limit이 많아서 그렇다고 하더라고요. 그러면 이거 전처리는 어떻게 했는지를 막 듣다 보니까 아.. 깨달은 거죠. 이게 0이 많다는 것을 고려하지 않고 전처리를 그냥 했기 때문에 생기는 문제라는 걸. 근데 이게 그분들만의 문제가 아니라 그 분야에서 전반적으로 하고 있던 실수였습니다. 그래서 이를 개선하는 방법을 찾는 연구를 했었습니다.  연구하면서 느낀 건 이런 식으로 생각보다 지구과학이나 의생명과학 등에서 비슷한 게 쓰일 수 있는 테크닉들이 많이 있습니다. 통계학의 장점이라고도 볼 수 있죠. 한쪽 분야에서 생긴 문제를 풀다가도 다른 분야에서 비슷한 문제를 발견하면 그쪽 분야에 가서 풀어도 해결할 수 있어요.

1) ibs 의생명 수학 그룹: ibs(Institute for basic science, 기초과학연구원) 수리 및 계산 과학 연구단에 속한 연구 그룹이다.
2) ODE(Ordinary differential equation, 상미분 방정식): 독립변수가 하나인 미분 방정식이다.
3) 노출군(exposed class): 병원체의 잠복기로 인해서 감염되었지만 아직 병원체의 전파 능력이 없는 개인들을 노출군이라고 한다.

8. 교수님을 계속 통계학자이게 하는 원동력은 무엇인가요?

통계학을 하면 앞서 설명했듯이 다른 분야의 과학 연구를 하시는 분들의 문제를 많이 풀어줄 수가 있어요. 그래서 지루할 틈이 없습니다. 지루할 틈 없이 다양한 연구를 할 수가 있다는 게 가장 좋은 것 같아요. 그리고 머신러닝 같은 것도 새로운 것들이 나올 때마다 통계학자로서 이해하기가 상당히 편한 것들이 많습니다. 결국은 머신러닝, AI도 경험적 데이터에 기반한 경험적 모델이다 보니까 통계학을 잘하는 사람들이 이해가 빠르거든요. 그런 부분에서 사후적이긴 하지만 통계학을 하길 잘했다고 느낄 때가 있습니다. 최근에는 베이지안 신경망(Bayesian Neural Network)도 각광받고 있는데 저는 베이지안 통계학자로서 이를 이해하는 게 훨씬 수월했죠. 머신러닝 방법론들이 통계 이론에 기반을 두기 때문에 그런 게 나왔을 때 빠르게 캐치업해서 연구할 수 있다는 게 좋은 것 같습니다.

9. 교수님의 MBTI는 무엇인가요?

전에 검사했을 때 ESFJ가 나왔습니다. T랑 F가 반반이긴 한데 그래도 ESFJ가 맞는 것 같아요(웃음).

10. 진로에 대해 고민하고 있는 학생들을 위해 조언 부탁드립니다.

일단 일이란 건 원래 다 힘듭니다. 어떤 일이든 직업이 되면 다 힘들어요. 힘들지 않다면 그건 직업이 아니고 보통 돈을 자기가 내고 하려고 하죠. 돈을 받고 하려는 게 아니라. 모든 일들은 다 힘든데 그중에서 자기가 진짜로 평생 혹은 장기간 하면서 견딜 수 있는 일이 어떤 것인지를 생각해봐야 해요. 예를 들어서 학계에 가는 게 너무 싫으면 가면 안되겠죠. 반대의 상황도 마찬가지이고. 저 같은 경우에는 그냥 학부 졸업하고 회사에 가면 가서 못하지는 않을 것 같은데 제가 그것을 평생 감당하는 건 싫을 것 같다는 생각이 들었어요. 그 직업이 나쁘다는 게 아니라 제 자신이 그걸 못할 것 같다는 생각이 들었어요.
 사람마다 적성이 다 다르기 때문에 자기가 덜 힘들게 할 수 있는 일을 찾아야해요. 근데 그것도 쉽지는 않습니다. 원래 어려워요. 저는 그래도 학계에서의 일이 만만치는 않지만 학계에서 겪는 어려움은 감당할 수 있을 정도의 일이라고 생각해서 일을 계속 하고 있는 것 같아요. 논문에 대한 압박은 그냥 ‘연구하면 되지’라는 마인드로 극복합니다. 어떤 사람은 저보다 훨씬 똑똑한데도 불구하고 지속적으로 일정 연구 성과를 내야되는 압박을 못 견디는 분들도 있어요. 직업이란 건 항상 힘들 수 밖에 없기 때문에 자기가 이 일을 얼마나 잘 감당할 수 있을까를 고민해봤으면 좋겠습니다.
ㅤ

11. 서울대학교 자연과학대학 학생들에게 한 말씀 부탁드립니다.

이제는 융합과학의 시대이기 때문에 자기 전공에만 국한되지 않고 활발하게 학문의 경계를 넘나드는 연구를 하는 게 지금 트렌드인 것 같습니다. 그래서 적극적으로 다른 분야에도 관심을 가지고 기회를 찾아봤으면 좋겠어요. 이것도 쉬운 일은 아니지만 그래도 그렇게 좋은 분야를 잘 찾으면 굉장히 큰 기회가 될 때가 있습니다. 그리고 특히 나중에 학자가 될 분들의 경우 다른 분야 공부를 해놓으면 나중에 연구를 하면서 정말 신기하게 도움이 될 때가 있습니다. 한 사람이 모든 걸 다 할 수는 없지만 그래도 다른 분야에 흥미가 있으면 경계를 조금씩 넓혀서 한 발자국 두 발자국 더 나아가서 해보는 것도 좋다고 생각해요. 그게 나중에 많은 도움이 됩니다(웃음).
ㅤ

참고문헌 및 사진 출처
ㅤ

1. Haran, M., Chang, W., Keller, K., Nicholas, R., and Pollard, D. (2017) Statistics and the Future of the Antarctic Ice Sheet, Chance, 30 (4), 37-44.

2. Chang, W., Haran, M., Olson, R., and Keller, K. (2014) Fast dimension-reduced climate model calibration and the effect of data aggregation, the Annals of Applied Statistics, 8 (2), 649-673.

3. Ham, YG., Kim, JH. & Luo, JJ. Deep learning for multi-year ENSO forecasts. Nature 573, 568–572 (2019). https://doi.org/10.1038/s41586-019-1559-7.

4. Zhao, S., Jin, FF., Stuecker, M.F. et al. Explainable El Niño predictability from climate mode interactions. Nature 630, 891–898 (2024). https://doi.org/10.1038/s41586-024-07534-6

5. Goes, M., Urban, N. M., Tonkonojenkov, R., Haran, M., Schmittner, A. and Keller, K. (2010). What is the skill of ocean tracers in reducing uncertainties about ocean diapycnal mixing and projections of the atlantic meridional overturning circulation? J. Geophys. Res.-Oceans 115 C10042.

ㅤ

 
자연과학대학 홍보기자단 자:몽 송주형 기자 (rachmaninoff@snu.ac.kr)
카드뉴스는 자:몽 인스타그램 @grapefruit_snucns에서 확인할 수 있습니다.